Differential Privacy - Sharing Insights Privately, In Public

21st October, 2019

9 min read

In a previous article I explained there is no such thing as anonymised data. If you don't want a privacy breach, don't release your dataset - in any form. As I explained, even statistical and demographic summaries of the data can be used in so-called reconstruction attacks to reveal information about individuals in the dataset.

_{Photo by Josh Rose on Unsplash}

But for some datasets - such as census data - it is a legal obligation to release statistical analysis. It is also a legal obligation to preserve the privacy of citizens who participated in the census, but releasing the required statistical analysis will breach privacy...

You're damned if you do, and damned if you don't!

computer science got us into this mess, can it get us out of it? - Latanya Sweeney

Privacy in the context of statistical analysis

Before we dive into what differential privacy is, we should look at what we - as potential dataset creators - should consider if we care about privacy.

Keep it private

It bears repeating - there is no such thing as anonymised data, so we know we must never release the raw data.

Differential privacy is not concerned with data warehousing nor security, we'll just wave our hands here and say "the data is never public".

Protect the individuals

We want to ensure that the presence, or lack, of an individual in a dataset will not expose any details of that individual - usually easier with a large dataset.

Limit the number of queries

While so-called reconstruction attacks cannot be used against differentially private functions, allowing unlimited queries is a de-facto privacy breach. The number of queries should be limited because we know each query results in a loss of privacy.

If we set an upper limit to how much privacy loss is acceptable, and we quantify the privacy loss of each query, then we have the basis of a privacy budget to limit queries from individual researchers.

Differential privacy

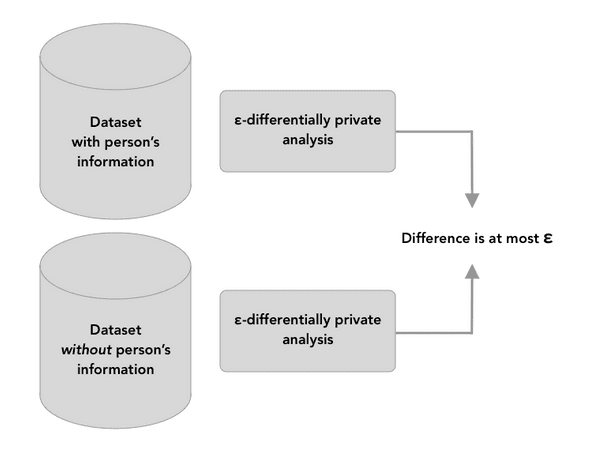
Differential privacy mathematically guarantees that

anyone seeing the result of a differentially private analysis will essentially make the same inference about any individual's private information, whether or not that individual's private information is included in the input to the analysis

Not only that, but the results of differentially private statistical analysis are immune to reconstruction attacks, linkage attacks, re-identification, and can be combined with other datasets - present and future - without exposing privacy.

That is amazing.

How do we do this?

We add noise.

But how much noise should be added? We want our dataset to be useful, but also preserve privacy. If we add a small amount of noise the statistical results will be very accurate, but the privacy of individuals will be threatened. If we add a lot of noise then the privacy of individuals is guaranteed, but the statistical accuracy will suffer and the data will be useless.

In order to achieve the most accurate statistical results while preserving privacy, it is vitally important to accurately calculate the minimum amount of noise.

Privacy loss parameter

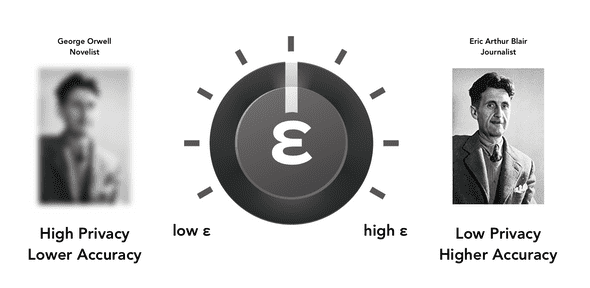
Each query made against a differentially private system will result in a loss of privacy, but as curators of the dataset we choose to set a maximum acceptable level of privacy loss using whatever criteria are relevant to the application. ε-differential privacy quantifies this maximum acceptable loss of privacy using the privacy loss parameter ε (epsilon).

ε - privacy loss parameter

The larger the value of ε the more privacy is lost. The variable ε quantifies the privacy loss for any query against an ε-differentially private system. A suitable value for ε could be between 0.1 and 1, although in practice much higher values are in use.

Sensitivity determines noise level

To determine how much noise should be added to the results of a particular query we need to figure out the sensitivity of that query. Sensitivity is a measure of the influence an individual's data can have on the output of a query. The higher the sensitivity, the higher the level of noise required to preserve privacy.

Imagine a small dataset containing the data of only 100 people. This means each person contributes roughly 1% of the total information. Clearly any query will have high sensitivity as the dataset is so small. We would need to add a lot of noise to preserve privacy.

Even in larger datasets queries can have high sensitivity. A query such as "billionaires with blue eyes, living in Florida, and taller than 1.8 metres" will have high sensitivity no matter how large the dataset.

It's straightforward to calculate the worst-case sensitivity of any query but more difficult to calculate the exact sensitivity of a particular query. This results in a higher level of noise than required to preserve privacy, and reduces accuracy of statistical analysis.

The accurate calculation of the sensitivity of queries is an important area of research as it aims to squeeze more accuracy from statistical queries against datasets while preserving privacy.

Privacy Budget And Composability

Each query made against an ε-differentially private function results in a loss of privacy, and as we said the dataset creator chooses the maximum acceptable privacy loss. It is possible for users querying the dataset to choose a privacy loss for each query that suits their needs as long as that privacy loss is less than the acceptable maximum privacy loss set by the dataset curator.

Researchers can choose to make many queries with low privacy loss, say 1 / 10 of ε, resulting in lower accuracy but higher privacy (ie. lower privacy loss for the individual) for each query, or choose a higher privacy loss and make fewer queries but with higher accuracy.

Privacy budget

Broadly speaking, you can track your privacy budget by adding together the fraction of ε used in each query. If you have made 10 queries each with a privacy loss which is 1/10 ε, then you can make no more queries as you have used your privacy budget.

A useful visualisation of this process is a hidden image revealed by uncovering random squares where the size of the square is determined by ε. You can see that smaller fraction of ε allows for more queries while still preserving the mystery of the hidden image. Queries using a larger fraction of ε would very quickly reveal the image.

_{Photo from Arif Riyanto on Unsplash}

Most queries, as described above, are known as sequential queries and simply add their privacy loss to the total used so far. There are also parallel queries that only add a single unit of privacy loss no matter how many queries are made in parallel.

Composability

The result of each query is differentially private, and the combination of query results is also differentially private - a valuable feature of differential privacy called composability.

Composability means that while each subsequent query does increase privacy loss, the queries cannot be combined in a way that will lead to privacy loss greater than the sum of all the privacy loss from queries up to that point. As mentioned before, ε-differentially private statistical analysis is immune to reconstruction attacks. If you make 10 queries with privacy loss ε you will only ever have 10ε privacy loss - incredible!

Group privacy

What we have been talking about up to this point has applied to the details of a single person. What if we are concerned with a group of people, such as a family? The same principle of composability applies to groups of people. The privacy loss of an individual is ε and the privacy loss of a group of people is kε where k is the number of people in the group.

Accuracy

We're adding noise, so how useful can any statistical analysis be?

The outputs from ε-differentially private functions are noisy. If you make the same query twice you'll get two different answers. Remember that smaller ε means larger privacy, and thus less accuracy, which in practical terms means more variation between results from the same query.

The query sensitivity has a large part to play in the accuracy of any analysis. We know queries against small datasets have high sensitivity, and thus require relatively more noise to preserve privacy. Similar queries against large datasets have relatively lower sensitivity and need less noise to preserve privacy.

Querying larger datasets result in more accurate results while preserving the same level of privacy.

Privacy washing

Just because a company is open about its approach to privacy does not mean it has your best interests at heart. I can forsee a lot of companies convincing people that their data is private and "safe", encouraging them to share more - this is just privacy-washing the fact that they are data mining their customers.

Apple, Google, and the U.S. Census are high-profile examples of ε-differential privacy in the real-world. The U.S. Census has been very open and clear about how they implement differential privacy, as has Google with regard to its RAPPOR technology. Apple, however, have been less forthcoming.

Despite data-mining issues, companies can badly implement differential privacy. This can either be from simple incompetence or by choice. It takes time and money to properly implement differential privacy - as mentioned before data security is essential. A company might choose to cut costs and knowingly use a poor implementation that leaks their customer's privacy.